Mostrar figures en un avió (definició)

2024 Autora: Leah Sherlock | [email protected]. Última modificació: 2023-12-17 05:30

La capacitat de mostrar correctament diferents formes al pla del full, el llenç i qualsevol altra superfície és una habilitat força important. I sobretot, és important tant per a persones d'art: pintors, escultors, artistes gràfics, dissenyadors (d'espais interiors i entorn arquitectònic), com per a persones de ciència: matemàtics, físics, dissenyadors, inventors.

Però també és important que una persona que està lluny d'aquestes esferes aprengui a percebre i mostrar correctament el món que l'envolta. Això ajuda a entendre molt més profundament tota la seva versatilitat. Si no teniu una idea suficient de com fer-ho correctament, és probable que no tingueu èxit en un projecte, imatge o dibuix de cap invenció. És a dir, aquesta habilitat és important tant per resoldre tasques senzilles i quotidianes com per a aquelles que tenen un significat global i universal.

Una mica d'història

Des de l'antiguitat, la gent ha intentat representar el que veia al seu voltant: altres persones, alguns edificis primitius d'aquella època, un món increïblement bell de plantes i animals, muntanyes majestuoses i simplement coses, articles per a la llar. És a dir, el món en tota la seva diversitat i grandiositat.

Però llavors encara no tenien ni idea de com es podia fer amb precisió i competència, de manera que la visualització de diversos objectes tridimensionals en un avió era realment realista, viva. La persona no tenia els coneixements pertinents i, a més, no hi havia habilitats especials, llevat potser de les més elementals.

En fonts anteriors es diu que la primera pintura del món consistia només en una línia que anava al llarg de l'ombra d'una persona projectada pel sol a la paret. És a dir, la pròpia naturalesa va suggerir en quina direcció val la pena avançar a la recerca de la solució adequada a aquest problema.

I aquesta pregunta preocupava l'home d'aquella època també per aquest motiu: no només volia admirar la voluminosa silueta viva, l'original, per dir-ho d'alguna manera, sinó que buscava captar un objecte espacial en un avió. I ho va fer perquè d'aquesta manera pogués decorar la seva casa o un lloc sagrat per a ell, o bé agafar-se un paquet amb una foto i traslladar-lo a qualsevol distància.

Geometria del patró

I digueu el que digueu, però van passar els anys, van passar els segles i, d'alguna manera, a mesura que es va desenvolupar la civilització, la gent va anar aprenent a mostrar figures complexes en l'espai bidimensional, és a dir, en un avió. Només que ara la precisió de les mides i proporcions dels objectes representats va començar a semblar molt aproximada.

Però la qüestió de la correcta visualització de la figura a l'avió i quant es corresponen amb el volum dels objectes originals, ja va ser molt rellevant. D'alguna manera, una nova ciència anomenadageometria. Més precisament, la seva secció és geometria descriptiva.

Aquí només està estudiant formes i plans, línies i punts, així com la seva relació entre si, tant en l'espai tridimensional com en l'espai bidimensional.

Mètodes de conversió

Una característica important de les arts visuals és la visualització de figures al pla de la imatge. Després de tot, de fet, es tracta de la captura d'objectes espacials tridimensionals en bidimensionalitat. És a dir: el complex s'ha de convertir en un de simple, és a dir, un objecte que tingui una llargada, amplada i alçada s'ha de transferir a un pla.

I la geometria descriptiva fa aquestes "transicions" gràcies a alguns mètodes. N'hi ha uns sis en total. Aquests són els tres principals i els més populars arreu del món:

• perspectiva (quan l'objecte representat s'elimina de l'espai);
• projecció ortogonal (projecció en paral·lel, on els raigs són perpendiculars al pla);
• projecció obliqua (projecció en paral·lel, on els raigs estan inclinats respecte al pla).

L'objecte representat apareix amb força claredat en projecció axonomètrica (que inclou ortogonal i obliqua). Però es projecta amb més claredat i veritat quan es mostra en perspectiva. I són els mètodes anteriors els que resolen en gran mesura la qüestió de com mostrar figures en un avió.

Perspectiva

La perspectiva ocupa el lloc més honorable entre altres mètodes d'imatge. Perquè l'ull humàcom una lent de càmera, veu l'espai circumdant d'una manera similar. Les coses que estan més allunyades de l'observador semblen de mida més petita, i de vegades molt més petites, que quan estan a prop.

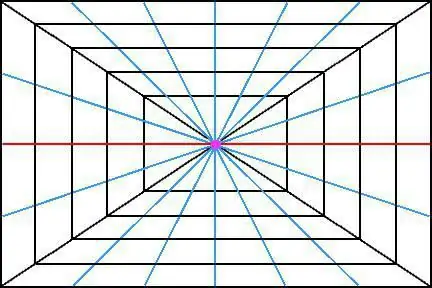
Per exemple, pren la imatge d'un cub a l'espai. Si, de fet, totes les seves vores són paral·leles entre si, aleshores quan mireu aquest objecte a la distància, pot semblar que les vores convergeixen (o haurien de convergir) en un punt. I, el que és més interessant, no només haurien de convergir en un punt, sinó que haurien de tenir un únic punt d'intersecció.

Gràcies als mestres del Renaixement: Albrecht Dürer, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti, la pintura moderna sap què és la perspectiva lineal directa, com determinar l'alçada de l'horitzó i els punts de fuga.

I el geni mundialment famós, Leonardo da Vinci, va argumentar per primer cop el concepte de perspectiva aèria. Això inclou un canvi en el color, el to de l'objecte, canvis en les seves característiques de contrast (disminuint a mesura que l'objecte s'allunya).

Projecció ortogràfica

L'ortogonal s'anomena projecció paral·lela, que es dirigeix a una recta, que és perpendicular al pla. En el procés de la seva aplicació, les dimensions dels contorns de l'objecte es mantenen sense canvis. És a dir, l'objecte es mostra sense distorsió.

L'objecte tridimensional projectat està, per dir-ho, descompost en tres vistes: des del costat, des del davant i des de d alt. I mirant tot això al mateix temps, podeu afegiruna representació de com és un objecte en volum. Al mateix temps, les dimensions de la figura es mantenen in alterables tant en la imatge tridimensional com en la bidimensional.

Projecció obliqua

Aquesta projecció es subdivideix en diverses subespècies més, a saber:

• visualització isomètrica;
• projecció dimètrica;
• projecció trimètrica.

Isometric té coeficients de distorsió en els 3 eixos (longitud, amplada, alçada). És a dir, els angles entre eixos agafats per parelles són iguals a 120 graus. En el dimètric, les distorsions al llarg dels 2 eixos són iguals, i el tercer és diferent. I a la projecció trimètrica, tots els coeficients de distorsió (és a dir, al llarg dels 3 eixos) són diferents.

Formes de gir

Quan un triangle rectangle gira al llarg de l'eix d'un dels dos catets, el seu tercer costat (hipotenusa) descriurà una nova figura anomenada con. I si feu girar un rectangle (quadrat) al llarg d'un dels seus costats, obteniu un cilindre. Quan el semicercle gira, sortirà una esfera.

Se'n dedueix que girant el pla al llarg d'algun eix, obtenim les anomenades figures de rotació.

Aquestes figures tenen un eix de rotació. Com es veuen a l'avió depèn de la seva ubicació en relació al nivell dels ulls. Per exemple, els costats superior i inferior d'un cilindre són essencialment cercles. I si els mireu en un avió, semblen el·lipses.

Però la tasca es fa encara més difícil si, quan es mostrafigures espacials sobre el pla, tenen un eix inclinat. En aquest cas, és important que els contorns dels cossos de revolució estiguin equidistants de l'eix d'aquest últim.

Una mica sobre el clarobscur

El clarescur té un paper important a l'hora de mostrar figures en un avió. Perquè el volum de l'objecte representat es crea no només a causa de les línies, sinó també a causa de la distribució correcta de la llum i l'ombra als seus costats. I després sembla força voluminós en el pla d'una superfície bidimensional.

Així, la visualització de figures a l'avió, la determinació de les seves mides, les característiques de la superposició correcta de la llum i les taques fosques són molt possibles gràcies als mètodes anteriors. I, el més important, aquests són mètodes realment provats a la pràctica, que utilitzen els principals experts del nostre temps.